MATLAB
1. Getting user input
A very useful and yet simple way of getting user input is by using the inputdlg function. It pops up a window with text fields for the user to fill and returns a cell array of characters with those inputs.
The function has four main arguments:
-
The text that appears above each input field (The number of texts also determines the number of inputs in the box).
-
The title of the dialog box.
-
The dimension of each input field (If a scalar value is used all fields will have that dimension).
-
The default value for each input field.
Let's create an example to learn how to use it. We'll pop up a dialog box for the user to write the length, width, and height of a box.
First, we create new variables to store the value of each of the arguments. Then, we call the function to output the result to boxDims:

The input dialog that we create appears with the default chosen inputs in the fields. We fill it with new values and then click ok:
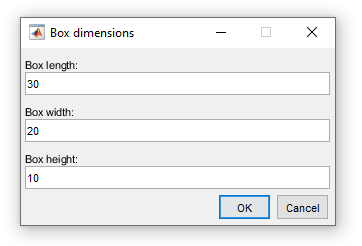

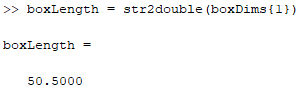
The values are stored as character vectors in a cell array. If we want to use one of them as a number, we have to convert it to a numerical variable. This can be done with the str2double function. Don't forget that to access the value of a cell array we use curly brackets { } and not parenthesis ( ):

Now that variable is ready to be used.
2. Solving equations
Matlab can solve equations and systems of equations, saving us time if we had to do it by hand. The function used for this is solve. It has mainly two arguments:
-
The equation(s) that we want to solve.
-
The variable(s) that we want to solve it to.
Let's see a real example. In the drawing robot project, we use the following equations to calculate the robot's X and Y coordinates on a whiteboard:


X and Y are the values that we want to find. The other three variables, dL, dR, and base, are constants given by the robot's initial coordinates.
First, we need to declare all these as symbolic variables so that Matlab will treat them as variables of an equation that can have multiple values and not as regular variables that have a constant value at any given time. To do this, we use syms:

Then, we write each of the equations as eq1 and eq2:

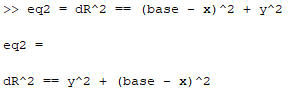
To solve them, we call the said function giving the equations we want to solve as the first argument and the variables that we want to solve it to as the second. We store the answers in new variables xa and ya:

Since we have two quadratic equations, we get two answers for each variable. The answers for X are equal and positive. For Y, because all the values represent lengths, which can't be negative, the answer will always be positive, so we'll only consider the second one. Therefore, we end up with:


In this case, to simplify the calculations, we can just find X first and then replace it on the first equation at the beginning of this section to get Y. So as final answers we'll use:


3. Converting units
It happens quite often that a value we want to use, usually a constant, is not in the same units that we're using on our project. Maybe we're using N.m and the value is in kgf.cm, or we're using gpm (gallons per minute) and it's in lpm (liters per minute), or maybe we're using inches and it's in centimeters.
Matlab has a function that allows us to easily convert from one unit to another. Here we'll obviously use it for engineering measurements, but it also works with other related values, such as currencies, for example. The function we're talking about is the unitConversionFactor. This function gives us the constant we should multiply our value by in order to convert it to the desired unit system. It has two main arguments:
-
The units of the original value.
-
The units that we want to change it to.
To use it, first we declare a measurement unit u. By using the object notation u.unit we can access whichever unit we want, and by multiplying a variable by it, we specify that that variable is in that unit. For instance, if we declare a variable a = 3, and then multiply it by u.m, which is the notation for meters, we determine that a = 3 meters:


Regarding the conversion itself, if we want, for example, to convert a torque unit value of 1,500 gf *cm (gram-force-centimeter) to N*m (Newton-meter), we can use the function to get the conversion factor:

Note that we had to multiply u.gf by u.cm to get our original unit gf*cm. We have to do this in case we're using a non-common unit that Matlab doesn't have ready in its system. The standard value is given in a fraction, but we can convert it to double if we want to:

Then, we multiply the factor by our original value in order to convert it:

1600 [gf*cm] = 0.1569 [N*m]
The simplest way to achieve this, however, is to do everything in one step:
