SELF-BALANCING
MOTORCYCLE: PART IV
1. Introduction
It's time to apply the knowledge from the previous sections to the real model. In this chapter, we'll implement a controller to make our motorcycle self-balance. We'll also implement some safety measures that are not required in simulations since nothing can break there, and lastly, we'll also drive it forward and backward and make it turn, which is something we haven't done so far.
2. Model Implementation
The model and controller that we're going to implement are exactly the same as before. However, because now we're working with real hardware, the layout may seem a little different, since we have different blocks and ways of connecting them. The general model is the same as before: as main blocks we have the motorcycle and the controller:

For the motorcycle, we read the raw values from the IMU (angle, velocity, and status), the battery (voltage), and pulses from the Hall sensor. We also have the motor command input for the reaction wheel motor there:

(click to enlarge)
To count how many magnets have passed in front of the Hall sensor, we do as we did in the first section when we tested the components: we use an interrupt pin from the Arduino board which goes as input to a function triggered subsystem:

There we have the simple counter below. Each time the sensor reads a south pole from a magnet, it goes to LOW and generates a pulse. This pulse interrupts the algorithm flow and triggers this function, which adds one to the counting. We also need a rate transition block since our model is running on a fixed step size and the function, which is triggered by the interrupt pin doesn't have one since it runs whenever an interrupt occurs.

You may have noticed that the other two motors, the one that drives the motorcycle forward and backward, and the servo, are not present in the plant block. Although it makes sense for them to be here, since they are part of the system and not the controller, we chose to keep them in the controller block. This is because the aim and hardest part of the project is to make the motorcycle balance, driving and turning it are simple secondary actions of the project that can be achieved with just a few blocks and pretty much no control logic, so we've kept them there in order to have it look clean and easy to understand.
Moving to the controller block, here's the overview:
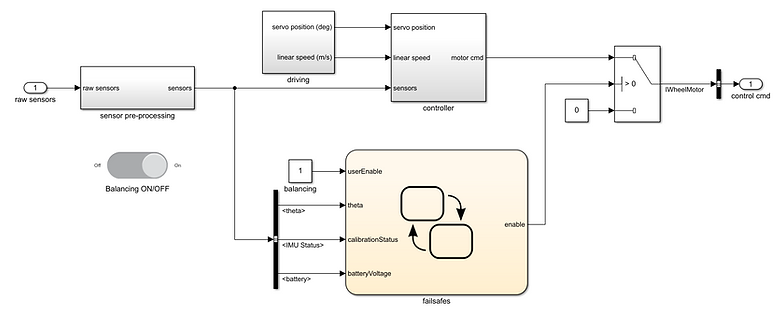
(click to enlarge)
In the first block, we process the raw signals that we read from the motorcycle. We route the correct one from the axis that matter to us, we add the bias offset to the angle reading if necessary, we transform the battery reading to a voltage reading and we calculate the inertia wheel velocity with the pulse count input the way we did in chapter one:

(click to enlarge)
The blocks and functions are the same as before, but we'll show them here again so that we keep the logic flow:

(click to enlarge)
First, we calculate the unsigned inertia wheel speed in RPM:

Then, we have a block to lock the first direction of the dc motor, which is also the first direction in which the wheel will turn:

And finally, we have a function that identifies direction changes and computes the current wheel velocity. Notice how the second "unit delay" block on the latch is necessary by looking at the condition of the first function "if-statement". The first time step in which the motor is on, we need the latch to still be zero (false), otherwise, that condition, which locks the motor direction, would never be met and the speed direction ("speedDir" variable) would remain zero forever.

Now we have the signals processed in the way and units that we need to be used by the controller, which we'll take a look at shortly. Before that, let's see a new feature that was added to this real-world model: the failsafe.
That are certain conditions in which we don't want the controller to work (i.e. the motor to be turned on) or we want it to be turned off if it's already on. These are:
-
If the leaning angle is too high (±6º), since the required torque will be outside what the motor can provide.
-
If the battery level is too low.
-
If the IMU is not calibrated.
-
If the user "Balancing ON/OFF" switch is turned off.
To implement this logic, we use a State-flow chart with states that run in parallel. Notice that for the battery and the IMU there's a latch, meaning that once the status changes it's impossible for it to go back until we restart the model on the hardware:

(click to enlarge)
We then have a switch in place so that if one of the conditions above is met, the inertia wheel motor is turned off by feeding zero to it instead of the controller command.

Inside the controller subsystem we also have the "driving" block, which implements the two logic for driving the motorcycle forward/backward and steering with the servo. Again, these are the same as the ones in the first chapter:

Regarding the steering, we don't change the angle instantly, but rather increase it linearly in order to don't provoke abrupt disturbances in the system:

(click to enlarge)
In the "linear speed" block, we calculate the motorcycle's linear velocity based on the encoder counts:

(click to enlarge)
Lastly, we have the controller block. Here the same logic was used, but the gains are different since now the output isn't the torque directly, but the motor's duty cycle ranging from -1 (-12V) to 1 (+12V). The contents of the "logging" box are only used to display the desired signals, and the ones inside the "turning" box will be used to calculate the optimal angle when the motorcycle is turning, but we can forget about it for now. When the linear speed is zero that angle is zero, so when it's self-balancing in place it has no effect at all on our controller. We also have put the bias slider here so that it's easier to adjust the gains and this offset on the same screen:

(click to enlarge)
With everything explained, let's proceed to test the controller.
3. Self-Balancing
The main objective of the project is to have the motorcycle balance in place, and that's what we're going to test now. We have obviously tuned the gains to achieve this performance. As we've seen before, the proportional gain related to the angle is what drives it back to the upright position. The derivative gain adds damping to the system and diminishes overshoot, and the proportional gain of the reaction wheel speed prevents the wheel from accelerating indefinitely when the system isn't perfectly balancing on 0º, which in the real world is always the case.
Let's see how it performs while seeing the sensor readings at the same time. In the video below, the first scope is the angle, the second the motorcycle's angular speed, the third the inertia wheel speed, and the fourth the motor command:
The system balances in place and responds well to the disturbances that we add by poking it. Let's also take a look at the scope where we plot how each of the three terms contributes to the final motor command:

The first thing that we see is that when not suffering disturbances, the motor torque remains close to zero as the net result of the positive inertia wheel speed term and negative angle term. Here it becomes clear and easy to see how the inertia wheel term prevents it from accelerating to "infinity" as we've mentioned before, which obviously would cause something to break. The differential term is generally close to zero and only has some weight when the disturbances suddenly change the angle, as expected. If we pay close attention, we can also notice how this term increases before the angular displacement does, which is exactly its function since it represents its rate of change, but it's nonetheless interesting to see in a real project.
Let's see it in action again, but this time with a frontal view:
With a yellow sticker on the inertia wheel, it becomes easier to see its behavior. Here's the controller terms plot:

And we notice the same thing: inertia wheel and leaning angle proportional terms net to about zero.
By analyzing the first plot, we can see the angle offset or bias, which indicates that 0º isn't the angle at which the motorcycle's weight pass through the center of mass. On the one run below, the bias is clearly negative, indicating that the center of mass is to the left of the vertical plane. Because of that, the system has to tilt to the right to achieve balance, going to a negative angle:

As we've seen during the Simscape simulations, this causes the inertia wheel speed to be higher. On the plot above it's around 300 RPM. If we then adjust the bias with the slider, we can achieve a better performance, such as the one below, where the balance is closer to 0º and the wheel speed is also closer to 0 RPM:

3. Driving forward and backward
Let's try to drive the motorcycle while balancing and pay attention to the readings. Here I'm using a slider to set the motor's duty cycle. You may notice some freezing in the readings, that's when I'm moving it and changing the duty cycle. Although it's not great visually, this small freezing doesn't affect the sensor readings at all, it just delays the display a little bit:
The system responds well to driving, even at high accelerations, when a higher motor torque is needed in order to keep it upright. A good thing is that the motor almost never saturate. A good motor operating range means that it won't overheat and it will last. Lastly, we'll move to steering.
5. Steering
The last function that we'll test is turning the motorcycle using the servo motor. Our servo isn't very good and is only able to change the angle in 10º to 15º increments, even though we implemented a system to change it smoothly. This sudden turn exerts a force on the motorcycle's body that the inertia wheel motor has to compensate for. What we were able to achieve was turning it in place and then driving it forward/backward:
Notice how the motor command is very high, even saturating, when the servo turns the fork and also when we move the motorcycle. The reason why we're not able to steer normally, like a regular motorcycle, is because our motor is not strong enough. The maximum torque (stall torque) it can provide is below the one that we would need to make turns without the motorcycle falling to the side.
When moving the motorcycle while turning, there's still one more thing that we have to take into account: the centripetal force. This force acts on the system, pushing it to the opposite side of the turn, so there's an additional torque acting on the wheel-ground axis while we're steering and moving forward/backward at the same time. The centripetal force for a rotating object is given by:

Where m is its mass, v is its linear tangential velocity, and R is the rotating radius. We'll call the centripetal forces in our system Fcb and Fcw for the body and wheel respectively. Let's use the drawing from section 2 to draw the free-body diagram and better visualize these forces:

A
B
C
The velocity and radius are the same for both parts, therefore the centripetal forces are:


By decomposing forces the same way that we did for the weight ones, and using the trigonometric identity sin (90º - θ) = cos θ, we'll get the following components:

A
B
C
The torques acting on the wheel-ground due to the centripetal forces are then:


Leaning to the side we're turning is a normal reaction when we're driving a bicycle or a real motorcycle. We do this to increase the torque due to weight and therefore compensate for the centripetal torque during the turn. After that, we go back to the upright position. If we don't, we may fall to the side if the centripetal torque becomes greater than the weight torque. With this system, we can aim to do the same thing: lean the motorcycle while turning. This will relieve the inertia wheel from having to generate enough torque to compensate for the centripetal one. The next step then is to find the optimal leaning angle.
If we consider no external torque, this optimal turning angle is the one with which the net torque is zero, or:
By replacing the variables for the respective torques, we get:

By grouping the common terms, we obtain:

Which becomes:

And finally:

With this equation, we realize that the optimal angle only really depends on the tangential velocity and turning radius. We already have the linear velocity, which we calculate from the encoder pulses, however, we still need to calculate the radius.
The radius that we need is the one for the displacement of the center of mass (cm). The diagram below is the motorcycle view from the top, where α is the steering angle, given by the servo. When it turns, the displacement of the front wheel has a radius that is always bigger than the one from the rear wheel. Lcm and Lfr are the distances from the base of the triangle (or the rear wheel) to the center of mass and the front wheel, respectively.
These radii form two right triangles from which we can derive some trigonometric relations:


If we replace the rear wheel radius on the last equation, we get:

And finally, the equation for the optimal leaning angle when turning is:

From the Simscape simulation, we can see exactly where the center of mass of the body and the inertia wheel are. The cm of the whole system will be somewhere in between them, closer to the one from the body. By measuring it on the 3D software, we get the following values:


Now we have every constant that we need to compute the optimal leaning angle when turning. If you recall, on the model, we've already implemented this:
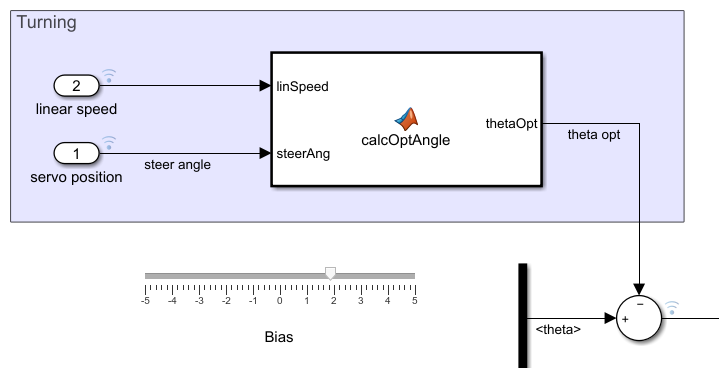
We have a function that calculates the optimal angle using the equations that we just derived and then adds this angle to θ. This offsets the leaning angle, so that the 0º around which the motorcycle balances is not really 0, but the optimal angle. Here's the function:

The faster and the smaller the radius, the greater the optimal angle has to be so that the net sum of the torques on the wheel-ground axis is zero. For example, if we're moving forward with a linear speed of 1 m/s, and we decide to make a 15º turn:

The optimal leaning angle would be about 6º. When the servo turned, we would subtract this angle from θ, so now its value is -6º and hence the controller would tilt the motorcycle to the left so that it goes back to 0º, which in reality if 6º. Obviously, this would happen incrementally, as the servo would not go from 0 to 15º instantly, and so wouldn't the optimal angle. If we had a nice servo and a stronger reaction wheel motor, we would be able to perform smooth turns. When finishing the turn, the opposite would happen and the motorcycle would become upright again. We may implement this in the future in a similar project.
6. Conclusion
This project is not as intuitive as it may seem at first. The way that the reaction torque is generated to keep the motorcycle upright is very particular and we had to spend some time thinking about it in order to really understand what's physically happening. We did however understand it and went on to develop it in three different stages: equation model, Simscape model, and real model. Here are a few things that we did on this project:
-
Work with DC motors and Hall sensors and calculate angular and linear velocity from the readings.
-
Derive the dynamic equations of a model using two distinct methods: Newton's Laws and Lagrange's Equations.
-
Simulate, log, and analyze the model behavior.
-
Create functions to plot the motorcycle's movement.
-
Create a state-space representation of our system.
-
Implement a full-state feedback controller to keep the motorcycle upright.
-
Analyze the influence of each state variable on the controller command and behavior of the system.
-
Tune the controller gains to achieve a desired performance.
-
Create equation-free simple and complex models by importing the 3D parts to Simscape.
-
Create 3D simulations that allow us to see exactly how the system is behaving, instead of just looking into plots.
-
Identify real-world problems that don't exist in ideal models and implement solutions to them.
-
Build a real model, implement the controller created in previous simulations and have the motorcycle successfully self-balance, even when subject to external disturbances.
-
Drive the motorcycle forward and backward and also turn.
-
Identify limitations of our project and how they could've been avoided (the servo is not precise enough and the reaction wheel motor should ideally provide more torque).