DRAWING ROBOT:
PART II
1. Introduction
In the previous part, we chose the motors' voltage supply and moved the robot by clicking buttons and pressing keys. Then, we calculated its final position based on a starting one. In this section, we'll do the opposite. We'll tell the robot where to go by giving it the desired coordinates and it'll move there. We'll then generalize this process so that it will move through a given set of waypoints. This will allow us to begin to draw simple forms on the whiteboard and it will be the same process that we'll use later to draw processed images.
2. Moving to desired coordinates
If you recall, the way that we calculated the robot's new position after moving it, was by transforming encoder pulses into string lengths. These lengths were added to the previously known lengths, and then, having the final length of both left and right strings, we computed its new XY coordinates using trigonometry.
To move the robot to a new given set of coordinates, we'll do exactly the reverse process: by knowing the new XY coordinates, we'll calculate how much string each motor has to wind/unwind, and by knowing the parameters such as the spool radius, the motors gear ratio and the encoder pulses per revolution, we'll ultimately know how many pulses each motor has to "turn" in order to move the robot there.
Let's use the diagram to visualize what we're doing and find the equations. We begin as before, from a known initial position. We measure and input each string length using the previously created function startingCoordinates. This will give us the full string length on each side, dL0 and dR0:
dWB

dWB - X
dL0
dR0
Y
X
dL
dR
known initial position
desired final position
The two right triangles formed by the desired new position will have the same previous equations:
Now, however, what we want to find are the distances dL, and dR, so it's much easier. We just have to square-root the other side of the equations:


Next, we have to subtract the initial string length values from these to know how much string each motor will have to wind/unwind. Since we are computing doubled strings, we multiply it by two:
Then, having the arc length, we find each motor's required angular displacement to get to the new coordinates:


We compute how many revolutions that is:


Finally, with the system's parameters we find the encoder counts:
We put this code into a function so that we can use it later if we want to:

Okay, this is how we calculate the amount each motor has to turn to move from one point to another. When drawing on the board though, our lines will be made of many points, so we'll have to perform this task repeatedly, and not just once. Consequently, we'll also need many input points, which will be the contour of the pictures, but for now, to test our calculations and develop an algorithm to move through these points, we'll get a set of waypoints from a user input instead of a processed image.
Let's write a function to pop up a window displaying the robot's initial coordinates and allowing the user to click on the coordinates for the robot to move to:

The function plots the chosen points as the user is clicking so that the path that the robot is going to draw is clear. When enter is pressed, it goes out of the loop and stores the waypoint's coordinates into an array. The blue dot is the starting position.



In this case, the user clicked 11 points to form the figure. The values are stores in an 11x2 matrix.
Before we develop an algorithm to move the robot through these points, we're going to anticipate a problem that we encountered. Since we're already talking about this function, it'll be easier to introduce it now. As you can see, in the images above the waypoints are far away from each other. The driving algorithm, however, works much better with points that are close to each other, so that the distance is so small that errors are minimized and the general shape of the object is maintained. In order to do this, we wrote a function to divide the line segments drawn by the user into smaller ones. Here's how it works:
Let's take as an example the line below and assume that we want to divide it into smaller segments:
0
xi
xf
X
yi
yf
Y
From trigonometry, we can write these two equations to find the line length and the slope:


Regarding the line, to find how many points we can fit into it we have to divide its length by the distance that we want between each point, and then round it down since it has to be a integer:

We then compute the distance between the fitted points:

If we subtract this value from the total length of the string and divide it by two, we get the distance that we need on each side of the line in order to center the points in it:

The diagram below makes it easier to visualize what it is that we're doing:


Finally, we calculate the X and Y values of each new point:

0
X
Y
Note that for the first point, the hypothenuse distance will be and the X and Y coordinates will be the first ones: xi and yi.
Here is the function that we've written to perform this task:


Let's apply it to the previously created figure. As you can see, this function prompts a window for the user to enter the desired distance between each point. Below are two examples, one where the chosen distance was 3 cm, and another where it was 0.3 cm:

distance = 3cm

...


distance = 0.3cm

...

Notice how the second one has almost around 9 times the number of points of the first. Below we zoomed in to better see how the points were fitted. The red circles are the original points clicked by the user. As you can see, they were all kept in the final figure. This is important to preserve its original form. In the case where we choose a very small distance between the points, it would be unnoticeable, but if the distance is not so small, it would erase the vertices of the image.

So far we have learned how to calculate the necessary number of encoder pulses to go to a desired position, and now we also have a tool to draw on the board and convert it to XY coordinates values. The next step is to generalize our first function to be able to calculate not only the encoder pulses to go to one point, but to a set of points.
To do this, all that we have to do is adapt the previous function to work with arrays Nx2 arrays instead of a 1x2 vector. Each line will contain the X and Y value of that point:

This time we will also output an array with the necessary angular displacement of each motor, in case we want to use angles instead of encoder counts in the future.
3. Motor control algorithm
Now that we can draw and find the coordinates of that figure, what's left is to implement an algorithm for the motors to move the robot through those points in order to draw it.
Unfortunately, this is a bottleneck to this project. The reason for that is that in order to drive the motors at the speed that we want, we'll need a controller, and in this particular case we'll be forced to use the built-in controller from the Arduino library, which doesn't work well at all. It's kind of an unpredictable black box and the particular function used to set the motor's speed is not even listed on Matlab's
We could develop our own, sure, but in order to do that, we would need to use Simulink. Matlab is more of an environment to do design calculations, plot results, and do math operations. When we want to test something in the real world, Simulink is the tool to use. It offers many tools and its visual programming environment allows us to drag and drop something that would require many written lines of codes. Therefore, it makes no sense for us to spend a lot of time building a controller in Matlab, and since we're not using Simulink on this project, we'll be saddled with the one from the Arduino library.
With that being said, we'll explain next what would've been the best solution to drive the robot from point to point on the board, and then we'll implement our own and see how it performs.
The main idea is to drive the robot from one point to another with a fixed linear velocity in order to have a smooth drawing that is accurate to the original. Let's begin with the diagram below. Since each arm is being pulled in the string direction, we have linear velocity components Vl and Vr there. The resultant linear velocity of the robot, V,is given by the combination of these two:
V
Vr
Vl
The reason why driving in a straight line from one point to the other is a challenge, is that as we know, the force on each of the left and right strings changes depending on the robot's position on the board. This means that the required torque is also changing, so we don't have a linear relationship between the voltage supplied and a corresponding motor speed. A second factor is that for the same reason, since the angles between the strings are changing as the robot moves, the direction of each linear velocity component is also changing. As we saw above, the resultant velocity is a combination of the two, so this means that in order to drive at a fixed velocity between the points, we'll need to constantly be changing the velocities components, and therefore the motors' velocities.
The velocity components' direction will be given by the strings. To calculate its magnitude we'll need to derive some simple equations. Let's start with the one below, where we're moving from one current point to the next. The points' positions will obviously be kept the same in all diagrams:

Y
current point
next point
Yn
X
Xn
0
It's clear that we can write the alpha angle using the definition of inverse tangent:

Next, we have the same diagram that we've shown before for any given robot position:
dWB

current point
0
-
X
Y
dWB - X
From this one we can see that:


The third one will be the one where containing the resultant velocity and its components:

current point
Vl
Vr
V
next point
Combining this diagram with the previous ones, we can conclude that:
Note that we can calculate the values of the angles beta and gamma because they depend only on the XY coordinates of the current and next point, which we have. Then, with gamma, we can find the last angle, phi. From the law of sines, we have that:

Now we can write the equations in terms of the linear velocity components:


What this means is that we would be able to calculate, based on the robot's current and next point coordinates, the linear components in order to drive with a resultant constant linear velocity. Finally, we can write the equations in terms of the motors' required angular velocity:


Remember that this would've been the case if we had, or could easily create, a motor speed controller. Since that's not the case, we'll work with what we have, but it's important to realize that this would've been the best solution for this project. The fact that we would've been able to drive with a constant linear velocity V, direct from one point to the other, would've kept the movement smooth, preventing variations to the left and right, and ensuring a straight line between points, which ultimately would produce the best accurate representation of our figure.
Now, let's see the solution that we've actually implemented. The controller that we are using is a function that takes as an argument the array with the number of pulses that each motor has to turn in order to go to all sets of coordinates, and then loops through them. Notice that the pulses counts are absolute values, which means they are computed from the robot's initial position. However, since we don't reset the encoders count at every iteration, when we calculate the difference between the current position and the next, we actually get the relative value.

p0 (starting position)
p1
p2
p3
p4
The most important thing is that our aim is to drive each motor at a given speed that is proportional to how many pulses it still has to "turn". Doing this ensures that each motor reaches its target value at the same time. This means that the drawn line, in theory, will be straight from one point to the other. That's not exactly the case here due to the limitations of the Arduino's library that we use to set the motors' speeds, as we mentioned before.
When the robot is within a certain chosen radius of the target point, it will move to the next. For example, imagine that in order to go from point A to point B, the left motor has to turn 300 pulses, while the right motor has to turn 500. If both turn at the same speed, we'll have the "faulty trajectory" below, because the left motor will reach its target value before the right one, which has to turn more. The result will be similar to the one below: the robot will first go up, and then it'll go right. What we want instead is a straight, diagonal line from one point to the other, which is achieved only when both motors hit their targets at the same time.
hit radius
optimal trajectory
faulty trajectory
B
A
The speed of each motor is calculated based on a desired maximum resultant speed Wref that is passed as an input argument. To calculate the speed proportions, we divide the remaining pulses each motor has to turn by their norm. We then multiply this fraction by the reference speed and finally use the built-in setSpeed function to drive (or at least try to drive) the motors at those speeds. Because of the way that this function was built, we have to turn the motors on and off each time that we want to set a new speed. In our case, this means that we have to turn them on and off at every iteration. As you will see when we actually draw something on the board, this constant switching causes the robot to shake a lot, and with it the marker, resulting in lines that are not as smooth as they could be with a proper speed control.
Here's the code of our controller:

Now let's see it in action. We'll use all the functions that we've created so far in a live script in order to get the user input points, crate more points in the segments, and then draw the figure:

The chosen distance between the points is 2mm. The first one will be this triangle:


And now let's draw this star:



The robot works as intended and draws an accurate representation of the figures. Due to the already mentioned bottleneck regarding the motor controller, in order to get a decent drawing we have to draw slower than we normally would. This minimizes the error caused by the shaking due to the constant starting/stopping of the motors and at the same time allows us to have a small hit radius, which also helps to produce a somewhat straight line between the points.
4. Performing motor torque analysis
When using dc motors in a project, it's important to know which torque the system will require from them in order to realize if the chosen ones are powerful enough to perform the task, and also not get damaged in the process. In this section, we'll identify the torque limit of our motors and calculate the required torque to move throughout all the points on the whiteboard. By doing this, we'll also identify which areas of the board we should not move the robot to.
We'll begin by determining our motor constants and finding its maximum allowable torque. Every motor manufacturer provides a datasheet with important information about the motors. Below we have an extract from the one for ours from which we'll get three important parameters: the rated voltage, the no-load speed, and the stall torque:

The rated voltage is the optimal voltage in which the motor was projected to operate for the best performance, and also the voltage with which the motor test was performed. The no-load speed is the motor speed when it's running free, with nothing attached to its shaft. And the stall torque is the torque limit for which the motor won't be able to rotate anymore because the load it needs to turn has become too high. For this motors, we have:


For a brushed DC motor, the torque T is given in terms of the armature current i, and the back emf voltage e in terms of the shaft speed w:

The torque and electric k constants are sometimes given in different units, but in consistent units, they are equal → Ke = Kt. The electric circuit of a DC motor is the following:

We can ignore the inductance since the electrical time constant is much shorter than the mechanical time constant determined by the rotor’s moment of inertia. This simplifies the analysis and the circuit equation becomes:
By solving the system given by the three equations we get the final motor equation that relates its speed and torque to the constant parameters:

Now we can use this equation for the two cases, no-load and stall torque, to finally find the motor constant and armature resistance:
No-load: T = 0

Stall torque: w = 0

To perform this and all the other calculations, and also to later visualize the data, we'll write a Matlab live script:

Note that to have the values in S.I. units, we converted the no-load speed to rad/s and the stall torque to N.m. Matlab has a versatile unit conversion function that we use for this. You can check a tutorial for details on how to use it.

The rated voltage for the motors is 12V, however, we're using a battery that supplies 11.1V. In a simple way to put it, since we're supplying less power to it, our stall torque will be lower than the one in the datasheet. Using the found constants, we calculate this torque. Also, it's a good practice to limit the motor torque to 30% of the stall torque in order to avoid causing irreparable damage to the internal components, such as the wire coatings and brushes. We do that and finally find the maximum allowed torque for our motor, which is 0.0604 N.m:

Now that we have the maximum torque value, we will calculate the necessary torque to move the robot from every position on the board to make sure that in no case it will reach the stall value. First, let's create a grid to represent the whiteboard. This is a XY limited coordinate system with a resolution, in our case, of 1mm:

Because the robot is being pulled down by gravity, the torque that the motors have to provide to pull it up is proportional to its weight. The weight force is divided between the two strings from where the robot hangs. As it moves around, the angles that the strings make with the vertical change, and so does the force acting on them, meaning that the necessary torque from each motor will change depending on the robot's coordinates.
Let's see the free-body diagram for the robot when it's not moving:

Fl
Fr
weight
Since we have a doubled string, the forces will be divided between them. We'll call these tenL and tenR, as in left and right tensions, so Fl = 2*tenL and Fr = 2*tenR. Let's see a cleaner diagram:
tenL
tenL
tenR
tenR
weight
=
Fl
Fr
weight
To simplify our calculations, we'll perform them with the forces instead of the tensions, and in the end we'll go back and convert them.
Since the robot is not moving, the sum of the forces acting on it has to be zero. We'll break them in X and Y components in order to be able to do the math. We'll call the angles that the strings form with the vertical thetaL and thetaR:
Fl
Fr
thetaR
thetaL
weight
Decomposing the forces in X and Y directions, we have for each arm:
Fl*cos(thetaL)
Fl*sin(thetaL)
thetaL
Fr*cos(thetaR)
Fr*sin(thetaR)
thetaR
Since the sum of the forces in each direction must be zero, we can write the equations:

Which replacing with the components for each direction yields:


And finally solving these two equations for the forces gives us:


Since we know the weight of the robot, the only variables we have to find are the angles. We can calculate them using the definition of tangent for any given X and Y coordinate:
dWB
X
dWB - X

Y
thetaL
thetaR
Therefore:


So far we have everything that we need to compute the forces, and consequently the tensions. Now, let's calculate how much torque each motor will need to provide in order to move the robot. Since only one of the strings wound by the motor through the spool, we will have:

spool


Tension
X
Torque
Using the pulley and therefore doubled strings is a good way to gain mechanical advantage and reduce the necessary torque to pull the robot. It cuts it in half in comparison with the case when we only have one string, as you can see by the fact that the actual force on each side equals two times the tension. We have, however, to turn it twice to pull it up the same amount.
Now we have all the equations to perform our calculations on Matlab. We'll use the grid to have the X and Y coordinates for the board. Then, using the equations, we'll compute the left and right tensions on every single coordinate, and finally, with the tension values, we'll find the required torque on all of those coordinates.

Note that in the end we store the maximum torque and also the difference between the right and right motor torques in a matrix. Let's visualize them in a 3D surface:



The plots show us a few important pieces of information. The first is that when it's getting closer to the top horizontal line of the pulleys, the required torque increases exponentially. On the image below, which is zoomed in and looking from the left side, it becomes very clear. If you recall, we didn't include the point Y = 0 in our grid, because it's a singularity. The tension there would be infinite because the robot wouldn't be supported from above. We can also notice this if we check our equations. The theta angle that we're measuring tends to zero in that condition. Since the sin of zero is zero, the equation doesn't make any sense. Another way to look at it is by looking at the free-body diagram. If the strings were to be completely horizontal, there would be no vertical force component to balance the vertical weight force. It's just a condition that's impossible to happen.
What will happen, if we try to move the robot to a position close to the top, is that at some point the required torque will be too high and our motor will stall. If we keep it running, it'll eventually get damaged. Our maximum allowed torque is around 0.06 N.m. We get past that limit way before getting close to Y = 0.
Regarding the torque difference map, it shows something that we could've guessed by looking at the equations. On the left side, tL is higher than tR, and the opposite happens on the other side. This means that the left motor needs to provide more torque when the robot is on the left side, and vice-versa, and it happens because when close to the edges, the theta angle formed with the opposite side increases. The denominator of our equation is equal to both left and right forces, but the numerator is proportional to the sin of that angle. So when close to the edges, the strings on that side have to lift a bigger part of the weight force.

What we mentioned above is interesting and important in order to understand the system, but the most important information for us is that on most parts of the board, where we intend to move the robot to draw, the maximum required torque is below our maximum allowed. By turning the plot around to better visualize it, we can see that indeed the necessary torque is way below our limit of 0.06 N.m.

If we prefer, we can also plot this data as a 2D graph. Depending on what we're trying to analyze, one way can be better than the other.



Next, we'll choose the areas where the robot should not move to and eliminate them from the graphs. To do so, we'll create a mask with the points that should be removed. The regions where we do not want the robot to go are: where the torque is higher than the maximum allowed, close to the pulleys (we choose a 6cm radius), and close to the bottom because our whiteboard is actually on the ground and the robot's body will touch it before reaching those coordinates:

Let's plot the modified figures:

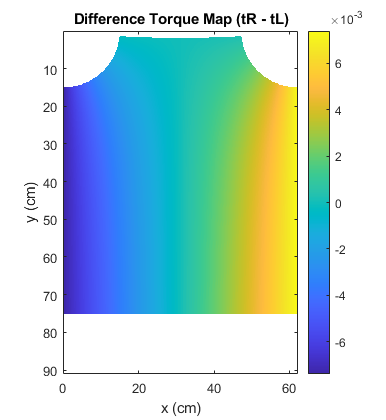
To finish the graphics, we'll choose a drawable region. Later, when we draw a processed image, we'll resize it to fit in this area:



It would be interesting now to see in the real world what we discovered here through the calculations. Let's run three tests on the robot to see if the behavior reflects what we've found.
The first one will be to prove that as we get closer to the top, where Y = 0, the torque demand increases. We'll start from a lower position and keep the same voltage supply through the process:
It's clear from the video that as the robot gets closer to the top the motors' speeds decrease, which is a consequence of the increase in the necessary torque to pull it up. The second time, when we have a higher voltage supply, the robot is able to climb a little higher. We don't keep the motors running for a longer period of time in order to not damage them, since when the motor speed is close to zero, the current is the highest because there's no back voltage (emf) opposing our battery's.
Let's now test if the motors need a higher torque when close to their sides of the board. We'll run three tests, one with the robot in the center, and one on each side of the board. Using the same equations as before, by counting the encoder counts we'll calculate how much string each motor wound and display it:
Here our findings also prove to be true. When on each side, that respective motor turns a lot less than the other one since it needs to provide more torque. Hence the shorter wound string length. Another way of noticing this is realizing that when a motor is on its side of the board, its string is almost vertical, so it has to turn a lot less to pull its side up because there's almost no horizontal component. However, in both cases we can notice that the other side is pulled up more than the one close to the board, again because the needed torque is higher so the motor turns less. Below is the comparison with the encoder counts and wound string for each case.
LEFT SIDE

CENTER

RIGHT SIDE

4. Conclusion
In this section, we saw how to implement an algorithm to move the robot to a desired position. This is known as inverse kinematics. We also saw how to implement a motor control to perform this task and some of its limitations that affect the drawing precision. Another important thing learned and that is a particular characteristic of this project was how the required motor torque changes as the robot moves to different coordinates on the board. The generated torque map is an excellent way to visualize what is need from the motors and helps us choose the right one. In the next part, we'll see how to process images to transform them into physical coordinates units that we can feed to the algorithm that we've created here in order to draw them on the board.